Point and space

 In continuation of the article "strange coincidence" here is a new exercise of geometric thought.

Thanks to Jean-Pierre and Adrien who kindly verified that the mathematical part was correct.

Let’s consider the 3D space geometric and continuous of the common sense. 
Let’s consider in this space a sphere S1 of diameter 1 
To facilitate the reasoning we will use a system of spherical coordinates originating from the centre of the sphere. 
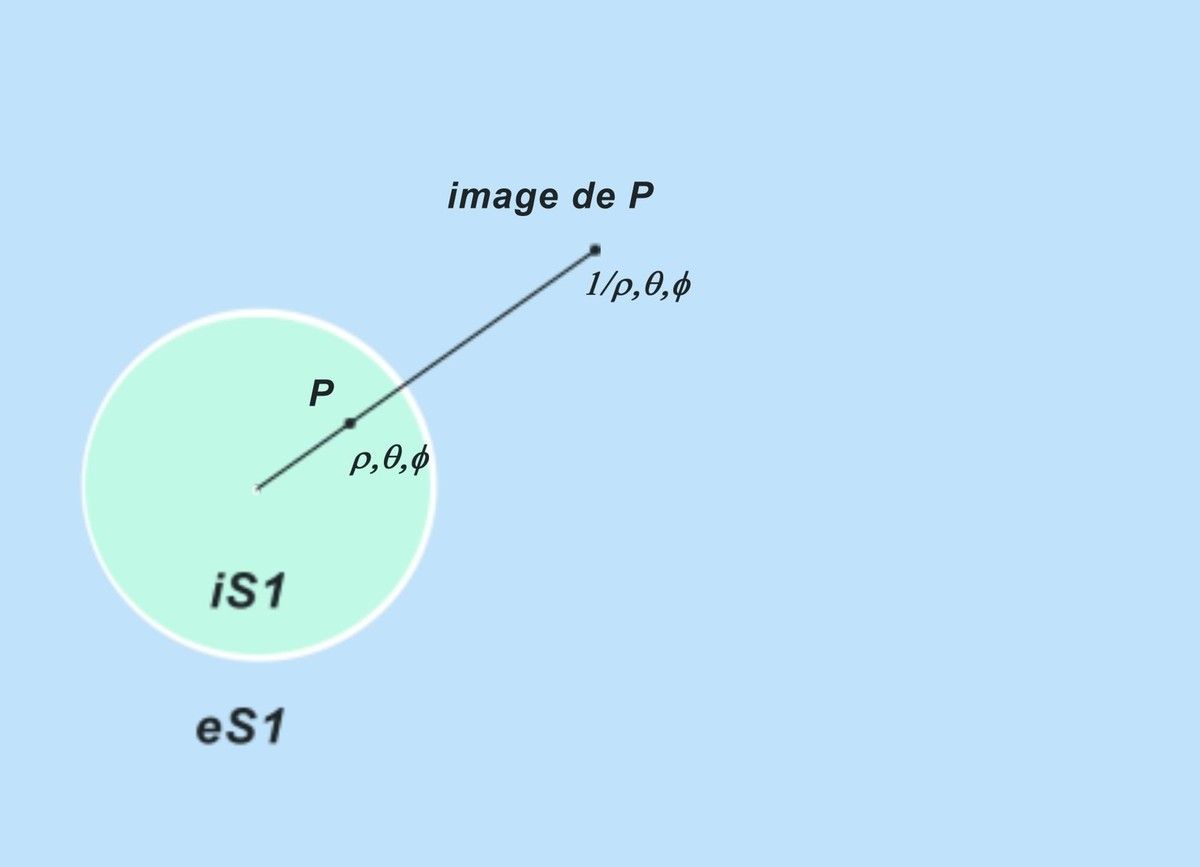
Let’s define an iS1 domain composed of the inside of the sphere without its centre or surface, 
Any point of iS1 will be identified by 3 coordinates, a length and two angles, (ρ, Θ, Φ) with   0 <ρ <1 

It is possible to associate with each point of iS1 of coordinates (ρ, Θ, Φ) a point of coordinates (1 / ρ, Θ, Φ) to form a domain which we will name eS1, the outside the sphere, 
This application from iS1 to eS1 has an inverse application. .  
There is therefore by this application, a bijection between iS1 and eS1 
2 consequences to that: 
..... iS1 and eS1 have are equipotent (simplified they have the same number of points) 
.... There is isomorphism between iS1 and eS1

It is therefore possible to map to any subset of iS1 a subset of eS1 and vice versa. 
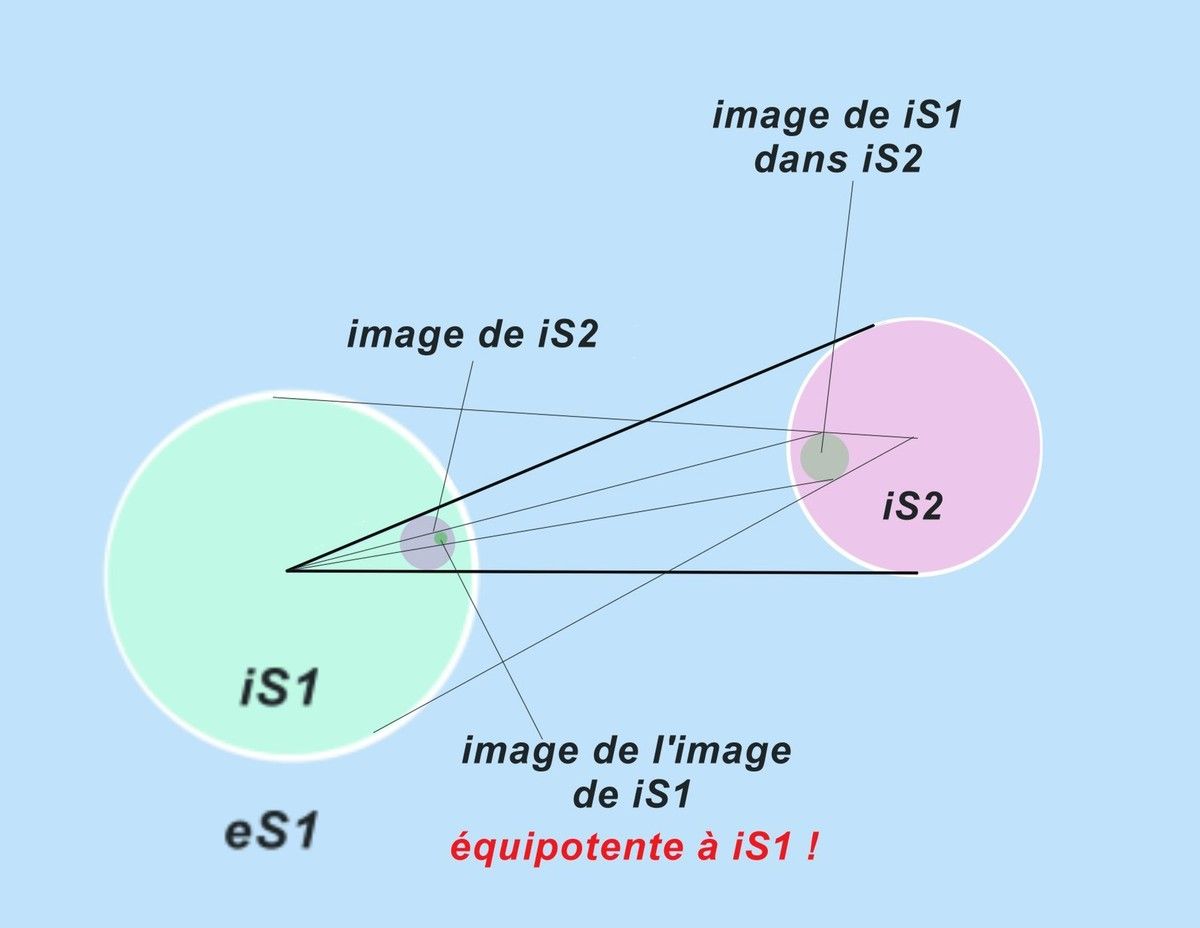
If for example we choose a sphere S2 of radius 1 entirely included in eS1, if we define the inside of S2 as a domain iS2 excluding centre and surface. We can map in iS1, the isomorphic and equipotent image of iS2.

Of course we could have carried-out the same reasoning from the sphere S 2 and create an image of iS1 inside S2 (included in the domain iS2) this image being isomorphous and equipotent to iS1.

By these two actions we would thus have: in iS1 the equipotent image of iS2 which itself contains the equipotent image of iS1.

That seems paradoxical: iS1 contains its own equipotent image.
Should we therefore renounce the millennial axiom of Euclid who says that "the whole is greater than the parts"?   (cf "Elements" 9th common notion)

In fact, there is no mathematical paradox here because the potence of a set (continuous and / or infinite) is not a measure of it and the relation of order "greater than" does not apply to potence. It is only possible to say "two sets in bijection are equipotent" 
Moreover, the theory of measurement takes this difficulty into account.

It should be noted that this example and its conclusions in a 3D space can be transposed to a plane (2 dimensions) or a line (1 dimension) but also to a 4-dimensional space (which one can not however immediately associate with the space-time of physics).

Should we abandon the bijection between continuous domains? 
Our problem would not be solved because the reasoning would lead to the same apparent paradox if we limited our space to the points of rational coordinates, the domains iS1 and eS1 (respectively iS2 and eS2) would then be countable infinite sets of points, so equipotent.

It is our desire to make of geometry an image consistent with the intuition we have of space that makes this paradox appear to us. Since the living has always existed in a universe where every spatial domain has content; we, living and conscious beings, see every point of space, every surface or line as "something". Like the content of the space. We are materializing space.

But this intuition of reality is uncertain, its coherence is approximate since it is based solely on our relative and approximate experiences.

Geometry and mathematics, as an epistemology of representation of the real, have for utility to highlight, to solve and to avoid the inconsistencies of their internal logic first, then between their theories and the immediate concepts which we draw from the experience of reality and finally, as much as possible, between their theories and our general intuition of objects in space. 
But these adjustments are not always possible or are not possible anymore. 
Thus, in the case of our exercise, mathematics show us that the point, defined as the limit of a series of spheres, has the same power as the space that contains it, while our general intuition makes us think the opposite. 
For anyone trying to solve this paradox, Ontology of Meaning recalls us that: 
1) The intelligibility and meaning reside in the point of view and not in "what is" in vis à vis. The shape of the observed object is only an unprovable concept. 
2) The meaning is a conjecture produced in and by the point of view. The only criterion of truth of meaning is the effectiveness of conjectures. This will be the only criterion for ultimately solving the inconsistencies between geometry and intuition of space.

The exercise presented by the article "strange coincidence" defines a "geometric point" as the limit of a series of spheres Sn whose ray is multiplied each time by a constant coefficient smaller than 1. 
Except for accepting the idea of ​​an actual infinite, this sequence has for limit a  "potential" point equipotent and isomorphous to the space which surrounds it, 
If the power is not a measure, it is none the less true that, since iSn and eSn can be put in bijection, to any "figure" of eSn can be associated an isomorphic figure in iSn. 
Anything that can be represented in "eSn can be represented" in "iSn. It is even possible to design for iSn an image coordinate system of a coordinate system for eSn. 
It will be noted that the definitions given by mathematicians to the real number are also based on the limits of convergent sequences and that therefore our paradox would appear as much to an analytical interpretation as to a geometrical vision. 
We are far from the simplistic definition of the non-breakable and dimensionless point. 
The definition of the point of our exercise is doubtless mathematically questionable. Nevertheless, ontologically, one can not ignore, at least as a conceptual hypothesis, the equipotence of the potential point and the space that contains it. 
The philosopher, as the mathematician will have to give up the infinitely small in act as the infinitely large in act. 
On the other hand, the equipotence between the potential point and the space which surrounds it poses to the philosopher the question of the foundation of reality. If we admit that the infinitely large is limited by a horizon, a limit whose cause would be in us, we must admit that the point is also limited by a horizon, and that behind this horizon is potentially an infinite complexity. 
Is the length of Planck the smallest measurable length in reality or the smallest conceivable length? 
This raises the question of the foundation of all logic: how to be certain that A = A if our knowledge of A is limited only by a horizon. How to prove that there is bijection in act between A and A?  
This questions even the topology of space-time: How to make sure that nothing that is "in" the point (4D) is also "out" of the point (4D).  

.

To make these questions more concrete, take the example of Special Relativity. 
In many texts, A. Einstein explains that the notion of simultaneity (dt = 0  ∀ x) is meaningless for distinct events and that the only invariant relations between events are the coincidence at a point in space-time ( dt = 0 and dx = 0) and the possible interconnection by a light signal. (dx = cdt). 
These statements are based on physical and non-geometric principles (equivalence of coordinate systems and constancy of c). 
For example, the emission or absorption of a photon is widely used by AE to represent a point in space-time. This approximation seems legitimate at the large scales envisaged by AE 
Yet this point of space-time corresponds to the definition of the potential point and not in act. The principle of equipotence point / space must therefore apply to its representation.

If one associates with the trajectory of the emitted light signal, a line coming out of the point of emission, the emission point must be regarded as equipotent to the full line.

If we associate the emitted light signal with a wave distributed in space-time, the emission point must be considered equipotent to this portion of space-time that is the cone of light.

Since the Lorentz transformation is analytical, how is it to be applied and interpreted to this part of the space that we represent as the interior of the point?

We have shown in the article " question of coincidence " that, in relativistic space, all the points of the trajectory of the photon coincide when they are represented in a frame linked to the photon. What about the inside of the emission and absorption points?

Is every point of the trajectory of the photon the equipotent image of the cone of light of which it is the summit?

 back to the list of articles